极坐标θ参数化方程的深入探索：其几何性质与动态行为解析

在当今数学与物理的研究领域，极坐标θ参数化方程以其独特的几何特性和动态行为引起了广大研究者的兴趣。极坐标作为一种重要的坐标系统，在描述圆形、螺旋线等图形时具有天然的优势。而参数化方程则为我们提供了一个动态变化的视角，通过改变参数值，我们可以观察图形如何随之变化，从而深入了解其几何性质和动态行为。本文将围绕这一主题，带领读者一同探索极坐标θ参数化方程的奥秘。

二、极坐标θ参数化方程的基本几何性质

1. 圆形轨迹的自然表达

在极坐标系中，参数化方程能够很自然地描述圆形的轨迹。例如，方程r=acos(θ)和r=asin(θ)分别表示以原点为中心的圆。通过参数θ的变化，我们可以直观地看到圆的形成过程，从而深入理解极坐标与圆之间的几何关系。

2. 螺旋线的动态展现

除了圆形，极坐标θ参数化方程还能很好地描述螺旋线的几何特征。例如，方程r=θ或者r=aθ等，通过改变θ的值，我们可以得到不同形态的螺旋线。这种描述方式不仅简洁明了，而且能够很好地展现螺旋线的动态生成过程。

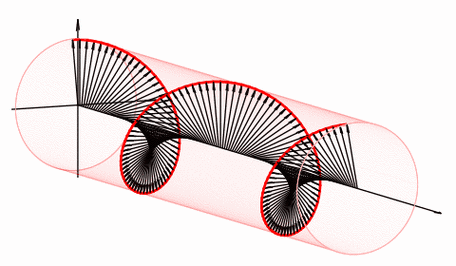
3. 参数变化对图形的影响

参数的变化不仅影响图形的形状，还影响其大小、位置等几何性质。通过深入分析参数与几何性质之间的关系，我们可以更好地理解极坐标θ参数化方程在描述几何图形时的灵活性。这也为我们提供了一种通过改变参数来设计和创造新图形的方法。

三、极坐标θ参数化方程的动态行为解析

1. 参数变化与图形的动态演变

通过改变参数值，我们可以观察到图形的动态演变过程。例如，在一个连续变化的参数下，一个圆形可能逐渐转变为螺旋线，或者一个静态的图形逐渐产生动态效果。这种动态演变反映了极坐标θ参数化方程的强大表现力。

2. 动力学中的应用

在物理学中，极坐标θ参数化方程被广泛应用于描述物体的运动轨迹。例如，在力学和电磁学中，许多运动可以通过极坐标θ参数化方程来简洁地描述和解决。这为我们提供了一种新的视角和方法来研究物体的运动规律。

3. 数学建模的重要性

极坐标θ参数化方程在数学建模中具有重要的应用价值。通过构建合适的参数化模型，我们可以模拟现实世界的各种现象，从而进行深入的研究和分析。这对于科学和工程领域的发展具有重要意义。

本文详细探讨了极坐标θ参数化方程的深入探索：其几何性质与动态行为解析。通过介绍其基本几何性质和动态行为解析的多个方面，我们深入了解了其在数学和物理学中的应用价值。随着研究的深入，我们还将发现更多关于极坐标θ参数化方程的奥秘和应用前景。希望本文能够激发读者对极坐标θ参数化方程的兴趣，为未来的研究做出贡献。